Der Plasmazustand der „weichen Materie“

Der Plasmazustand der weichen Materie

Pierre Gilles de Gennes, der 1991 den Nobelpreis in Physik erhielt, definierte “weiche Materie” wie folgt: “sie ist supramolekular, makroskopisch verformbar, enthält mikroskopisch angeregte Zustände, kann durch externe Kräfte in neue Phasenzustände versetzt werden und befindet sich physikalisch weit außerhalb der Quantenniveaus im klassischen Bereich.” Zur weichen Materie gehören unter anderem granulare Festkörper, Gele, Schwämme, Polymere, Kolloide usw. Es war nicht bekannt, dass es auch einen Plasmazustand gibt – und auch nicht erwartet.

„Komplexe Plasmen“ [1-4] bestehen aus einem Gemisch von Elektronen, Ionen, Neutralgas und geladenen supra-molekularen Partikeln. Es sind diese Partikel, die aufgrund ihrer starken elektrostatischen Wechselwirkung kooperatives Verhalten, Selbstorganisation und Strukturbildung erzeugen – und damit die oben genannten Eigenschaften der weichen Materie abbilden (Abb. 1).

Das Forschungsgebiet der Komplexen Plasmen hat sich seit der Entdeckung 1994 [5-7] rasant entwickelt – eine Popularität, die sich aus verschiedenen Faktoren zusammensetzt:

Die Systeme sind optisch dünn (das Verhältnis Teilchengröße/Teilchenabstand ist ~0.01) und sind daher visuell leicht zugänglich; die relevanten Zeitskalen (Plasmafrequenz, Einsteinfrequenz) liegen im Bereich von etwa 10 ms und sind leicht messbar, die Systeme sind aufgrund der Partikelgröße, Form und Material sehr vielfältig, sie sind leicht manipulierbar, kaum gedämpft und damit insbesondere für die Erforschung dynamischer Prozesse, nichtlinearer Wechselwirkungen, kritischer Phänomene usw. sehr gut geeignet. Sie beinhalten als neu entdeckter Materiezustand – neue und interessante physikalische Prozesse, z.B. nicht Hamilton’sche Wechselwirkung, Visko-Elastizität, Elektrorheologie, nicht-Gleichgewichts-Phasenübergänge usw., Eigenschaften, die zwar teilweise aus anderen Systemen (z.B. Kolloiden) ebenfalls bekannt sind - allerdings meist andere physikalische Ursachen haben und bisher dynamisch nicht messbar waren. Es ist der Reiz dieser Forschung, unser Wissen über die generischen Ursachen von Selbstorganisation, Strukturbildung, Universalität, Skalierungseigenschaften usw. auf dem elementarsten Niveau, der Bewegung einzelner Partikel im kooperativen Ensemble, zu vergrößern und somit ein fundamentales Verständnis dieser faszinierenden und grundlegenden generischen Prozesse zu erlangen.

Neueste Beispiele aus der Forschung

Der Rest dieses kurzen Berichts beschäftigt sich mit einigen Forschungsergebnissen aus neuester Zeit, wobei wir uns nur auf die Untersuchung von Flüssigkeiten auf dem (diskreten) Partikelniveau und den Prozess der Kristallisation in zweidimensionalen Membranen beschränken. Die Frage – ganz zu Anfang – ist natürlich: wie relevant sind flüssige Komplexe Plasmen im Zusammenhang mit generischen Eigenschaften von Flüssigkeiten? Falls es Gemeinsamkeiten gibt, bieten Komplexe Plasmen einen neuen Zugriff auf fundamentalstem Niveau! Dazu sei erwähnt, dass in Komplexen Plasmen die Wechselwirkung der Partikel untereinander dominieren: es handelt sich also um das bei weitem beste praktisch ungedämpfte „Ein-Komponenten-System“, welches kinetische (Teilchen-) Messungen erlaubt. Also ist die Erforschung von Instabilitäts- Transport- und Selbstorganisationsprozessen mit flüssigen Komplexen Plasmen in jedem Fall ein Gewinn.

Oberflächeninstabilititäten und Turbulenz

Die Entstehung von Turbulenz – der Übergang von regulärer geordneter laminarer Strömung zu ungeordnetem Fließverhalten - ist nach wie vor „das wichtigste und faszinierendste ungelöste Problem in der Hydrodynamik“ (Zitat: Richard Feynman). Da alle Flüssigkeiten aus stark wechselwirkenden Partikeln bestehen, ist die Erforschung von Instabilitäten im Grenzfall diskreter Systeme von ähnlich weit reichender Bedeutung – und vielleicht hilft dies sogar, ein grundlegendes Verständnis für die Turbulenz aufzubauen, Um diesen bisher experimentell (fast) nicht erforschten Bereich zu untersuchen, wurde am MPE ein umfangreiches Forschungsprogramm entwickelt mit dem Ziel, erstmals Präzisionsmessungen auf kinetischem Niveau durchzuführen. Solche Messungen können teils auf der Erde durchgeführt werden, teils benötigt man Schwerelosigkeit (die benutzten Partikel sind 10-100 Milliarden mal schwerer als typische Gasatome). Deshalb betreibt das MPE zusammen mit russischen Partnern vom Akademieinstitut IHED seit 2001 Experimente auf der Internationalen Raumstation.

In Abbildung 2 ist ein Messergebnis aus diesem Programm gezeigt. Es handelt sich um die Umströmung eines Widerstands. Die klassischen Regionen – laminare Strömung, instabile Grenzfläche und Wirbelzone sind deutlich erkennbar. Die Reynoldszahl (Strömungsgeschwindigkeit / (viskose) Diffusionsgeschwindigkeit) betrug ~160, lag also unterhalb der üblichen Größe für das Auftreten von Turbulenz von ca. 1000. Trotzdem treten an den Grenzflächen nichtlineare Instabilitäten (verglichen mit dem mittleren Teilchenabstand Δ) auf. Die Skalierungen sind: laminare Strömung L_e ~ 30-40 Δ, Fluktuationsbereich niedriger Amplitude L_f ~ 30-40 Δ, nichtlinearer Bereich mit linear ansteigender Amplitude (A) und Klumpung ~ A ~ ½ z. Interessanterweise ist die Skalierung in makroskopischen Strömungen ähnlich: der laminare Bereich ist typischerweise von ähnlicher Länge wie der einfache Wirbelbereich, ehe dann das nichtlineare turbulente Regime mit ähnlichem Amplitudenwachstum folgt. Natürlich kann dieses Skalierungsverhalten vom diskreten bis zum makroskopischen Bereich Zufall gewesen sein. Es müssen systematische Messungen bei unterschiedlichen Reynoldszahlen und verschiedenen kinetischen (Komplexe Plasmen) Systemen durchgeführt werden, um eine etwaige Systematik sicher zu identifizieren. Aber, in Richard Feynmans Worten, das Problem wird dadurch noch faszinierender!

Skalierungsverhalten zweidimensionaler Flüssigkeiten

Dreidimensionale Flüssigkeiten haben eine eigene (z.B. fünfeckige) instantane Symmetriestruktur, ganz anders als die der Festkörper (z.B. Messungen an Blei, [10]). Diese Erkenntnis ist von großer Bedeutung für das Verständnis der fundamentalen Stabilitätsprinzipien kondensierter Materie. Was aber passiert, wenn das System eingeschränkt wird, z.B. zweidimensionale Membranen, dünne Streifen oder gar eindimensionale Fäden? Topologisch, das wissen wir, wäre ein eindimensionaler flüssiger Faden von einem festen nicht unterscheidbar – dynamisch schon. Das legt natürlich nahe, die Systeme im Plasmenraum der kanonischen Variablen (x, v) zu betrachten. Allerdings ist es auch interessant, nur die Struktur zweidimensionaler Flüssigkeiten bei der Kristallisation zu untersuchen. Auch hier bieten sich Experimente mit komplexen Plasmen an. Abbildung 3 zeigt die dabei gewonnenen Ergebnisse.

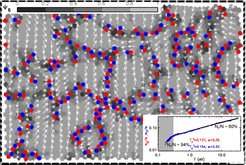
Es zeigt sich, dass zweidimensionale Systeme keine eigene Flüssigkeits-Symmetriestruktur haben. Die Struktur ist immer instantan im (energetischen) kristallinen hexagonalen Grundzustand. Bei höheren Temperaturen entstehen mehr und mehr Defekte, dabei auch hier „nur“ die nächst höhere Anregung – Paare von 5-und 6-Ecken. Interessant ist der Temperaturverlauf dieser Defekte – ihr Anteil steigt mit einem Potenzgesetz ~T^1/3 an, und das über einen sehr großen Skalierungsbereich! Die klassischen Theorien vermögen dieses Ergebnis nicht zu erklären – wohl aber eine neue Theorie, in der das System instantan als Zusammensetzung verschiedener (fraktaler) kristalliner Zellen, berandet durch 5/7 Dislokationsgrenzen, beschrieben wird. Diese „fraktale Hypothese“ könnte mit der Renormalisierungstheorie [12, 13] verknüpft werden, in der ein bestimmtes (Grenz-) Energiefunktional F (L+SL) durch ein anderes F (L) über eine Rekursionsrelation erzeugt wird.

Elektrorheologische Plasmen

Elektrorheologische Flüssigkeiten sind bekannt und werden zum Teil schon industriell eingesetzt (z.B. in Stoßdämpfern, Photonik). Dass Plasmen elektrorheologische Eigenschaften besitzen können ist allerdings gänzlich unerwartet.

In Kolloiden entsteht Elektrorheologie (elektrisch gesteuerte Strukturveränderung) z.B. durch starke von außen angelegte elektrische Felder. Die Kolloidpartikel werden polarisiert, mit ihren Dipolachsen parallel zum äußeren Feld. Das bewirkt, dass die Partikel sich in Linien hintereinander anordnen und führt zu stark veränderten Eigenschaften (Viskosität, Festigkeit, usw.). Diese Veränderungen sind schnell (hundertstel Sekunde), damit sind elektrorheologische Systeme vielseitig einsetzbar.

Neue Experimente auf der Internationalen Raumstation, z.T. vom deutschen Astronauten Thomas Reiter durchgeführt, haben jetzt gezeigt, dass komplexe Plasmen auch elektrorheologische Eigenschaften haben können (Abb. 4).

Allerdings ist der Prozess in Plasmen ein Anderer als in Kolloiden. Das ist nicht verwunderlich – die Systeme sind sehr unterschiedlich. In Kolloiden sind es die induzierten Dipole, die die dicht verteilten Partikel „steuern“, in komplexen Plasmen ist es die Fokussierung der Ionenströme um die Partikel herum, die im Mittel ein Quadrupolfeld erzeugen (innen repulsiv, außen attraktiv) und dadurch die dünn verteilten Partikel räumlich ordnen.

Die hier gezeigte Möglichkeit, das binäre Wechselwirkungspotenzial zwischen den Partikeln auf solch einfache Weise von außen zu „steuern“, eröffnet viele neue Chancen mit Komplexen Plasmen fundamental generische Prozesse experimentell zu erforschen. Vielleicht wird es sogar irgendwann gelingen „Designer-Systeme“ zu generieren, um ganz gezielt neue Materialeigenschaften zu erforschen oder sogar zu erzeugen.

Zusammenfassung

Komplexe Plasmen – der Plasmazustand der „weichen Materie“ – sind ein junges Forschungsgebiet von faszinierender Breite und hochinteressanten experimentellen Möglichkeiten Neues über wechselwirkende kondensierte Materie auf dem elementarsten Niveau zu lernen. Das Gebiet ist noch sehr jung, hat aber enormes Zukunftspotenzial.