Komplexe Plasmen als Modellsystem für kinetische Untersuchungen

1. Einleitung

Komplexe (staubige) Plasmen ermöglichen es, eine Vielzahl von Phänomenen auf dem elementarsten Niveau, der kinetischen Ebene zu studieren (vgl. dazu auch [1,2]). Komplexe Plasmen bestehen aus Ionen, Elektronen, stark geladenen Mikropartikeln ("Staubkörner") und Neutralgas. Die Ladungen der Staubpartikel sind nicht konstant ebenso wie die Plasma-Abschirmlänge. Das ist der Grund, weshalb die Stärke der elektrostatischen Koppelung zwischen den Staubteilchen leicht über einen ziemlich weiten Bereich geändert werden kann, beispielsweise durch Änderung der Entladungsbedingungen [3]. Das ist ein charakteristisches Merkmal Komplexer Plasmen gegenüber gewöhnlichen Plasmen, bei denen die Ladung der Ionen normalerweise konstant ist und die Ionen nur einfach geladen sind (Letzteres impliziert eine geringe Koppelungsstärke in normalen Plasmen, obwohl man prinzipiell in nicht-neutralen Plasmen eine relativ starke Koppelung erreichen kann, z.B. in Ionen-Kristallen). In Komplexen Plasmen kann man Übergänge von ungeordneten schwach gekoppelten Zuständen zu stark gekoppelten Zuständen beobachten, sowie die Ausbildung geordneter Partikelstrukturen - den Plasmakristallen [1,2,4,5].
Ein anderes charakteristisches Merkmal Komplexer Plasmen ist die Tatsache, dass die zur Dynamik der Staubkomponente gehörenden Zeitskalen relativ lang sind (Plasmafrequenz der Staubpartikel ca. 10-100 Hz) [1]. Ferner sind die Partikel selbst groß genug, um leicht einzeln sichtbar gemacht zu werden. Alles in Allem ermöglicht dieses eine Untersuchung von Phänomenen, die in verschiedenen Zuständen auftreten, auf dem elementarsten Niveau, der kinetischen Ebene [2,3]. Die Dämpfung, verursacht durch Reibung mit dem Neutralgas, ist um viele Größenordnungen kleiner als in flüssigen Suspensionen von Kolloiden. Auf jeden Fall kann man die Dämpfung in Komplexen Plasmen viel kleiner als die meisten Eigenfrequenzen der Dynamik der Staubpartikel machen, und infolgedessen haben die interessantesten dynamischen Phänomene üblicherweise genügend Zeit sich zu entwickeln [2].
Im Folgenden behandeln wir die neuesten Entwicklungen in der Kinetik Komplexer Plasmen und demonstrieren die Bedeutung dieses Gebiets für interdisziplinäre Forschungen.

2. Phasendiagramm Komplexer Plasmen

Abbildung 1 zeigt verschiedene Phasenzustände Komplexer Plasmen als Funktion des elektrostatischen Kopplungsparameter Γ_ES und des mittleren Partikelabstands Δ, normiert jeweils auf die Partikelgröße a bzw. Abschirmlänge λ ("Ordnungs-parameter" α=Δ/a und "Gitterparameter" κ=Δ/λ entsprechend) [6]. Der Parameter Γ_ES=exp(-κ), der das tatsächliche Koppelungsverhältnis (Potenzielle Energie / kinetische Energie) bei einem mittleren Teilchenabstand Δ beschreibt, kann durch die (Coulomb) Kopplungsstärke Γ=e²Z²/ΔT ausgedrückt werden (wobei Z die Ladung und T die thermische Energie der Staubpartikel ist). Die Verwendung von Γ_ES bedeutet, dass die Berechnungen einigermaßen repräsentativ sind, auch für andere Wechselwirkungspotentiale ähnlichen Typs (d.h. mit ähnlichen lang- und kurzreichweitigen Asymptoten). Die vertikale Linie bei κ=1 teilt das Diagramm in die Bereiche "schwach abgeschirmt" (Coulomb-Bereich) und "stark abgeschirmt" (Yukawa-Bereich). In Abbildung 1 setzen wir λ/a=α/κ=100, ein Wert, der typisch ist für die bisher untersuchten Komplexen Plasmen. Prinzipiell lässt sich aber der Wert über einem großen Bereich variieren, abhängig von der Größe der Partikel und den Plasmabedingungen.
Die Kristallisation in Komplexen Plasmen sowie die Ausbildung verschiedener Gittertypen sind häufig beobachtete Prozesse [4,5]. Vom phänomenologischen Standpunkt aus betrachtet ist die Bedingung für das Auftreten der Kristallisation im Wesentlichen durch die altbekannte Lindemann-Bedingung bestimmt [7]. Daraus leitet sich die in Abbildung 1 gezeigte Schmelzlinie (die obere durchgezogene Linie) ab.

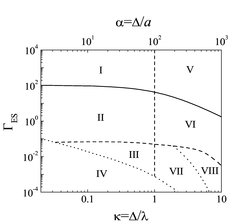
Tieferen Einblick in die möglichen Phasenzustände erhält man, indem man - wie in Abbildung 1 gezeigt - die Berechnung des Wirkungsquerschnitts für Impulsübertrag σ, auf die Staub-Staub-Stöße anwendet. Dieser Ansatz erlaubt eine klare physikalische Einteilung Komplexer Plasmen [6]. Die gestrichelte Linie zeigt den Übergang zwischen "idealen" und "nicht-idealen" Plasmen. Man erhält diesen Übergang aus der Bedingung (σ/π)^1/2=(4π/3)^-1/3Δ, die bedeutet, dass die charakteristische Reichweite der Partikelwechselwirkung (hinsichtlich des Impulsübertrags) vergleichbar ist mit dem Partikelabstand (hier der Wigner-Seitz-Radius). Oberhalb dieser Linie gibt es im Wesentlichen nur Mehrfachstöße, wohingegen unterhalb dieser Linie nur Zweierstöße von Bedeutung sind. Dieses verfeinert die Standardbedingung, die benutzt wird, um eine Grenze zu definieren zwischen idealen und nicht-idealen Plasmen, Γ_ES ~1. Aus Sicht der Thermodynamik bestimmt diese Linie die Grenze, bis zu der eine Entwicklung (z.B. Virialentwicklung) der thermodynamischen Funktionen nach dem (kleinen) Kopplungsparameter sinnvoll ist. In diesem Zusammenhang ist es wichtig in Erinnerung zu rufen, dass die Thermodynamik für ein Yukawa-Potenzial (ebenso wie für jedes monotones Wechselwirkungspotenzial) vorhersagt, dass es keinen Phasenübergang von flüssig nach gasförmig gibt, d.h. der kritische Punkt tritt in solchen Systemen bei T_cr=0 auf. Dies ist anders, wenn das Paar-Wechselwirkungspotenzial nicht monoton ist, also beispielsweise eine langreichweitige anziehende Komponente einem abstoßendem elektrostatischem Potenzial hinzugefügt wird. Theoretisch sind solche attraktiven Potenziale für Komplexe Plasmen vorhergesagt, aber bis jetzt gibt es noch keine verlässlichen Experimente, die das Vorhandensein von beispielsweise einer Koexistenz von flüssiger und gasförmiger Phase zeigen oder andere Indizien für Phasenübergänge erster Ordnung in gasförmigen Komplexen Plasmen liefern.
Die Bereiche, in denen das System einem granularen Medium ähnelt, sind ebenfalls in Abbildung 1 dargestellt: Im Bereich unterhalb der unteren gepunkteten Linie ist die elektrostatische Wechselwirkung zu schwach und der Impulsaustausch geschieht aufgrund von Staubkollisionen, d.h. wir haben das übliche granulare Medium, in dem Ladungen keine nennenswerte Rolle spielen. Die obere gepunktete Linie markiert den Rand einer sehr interessanten Region des "Yukawa granular medium", in der die stark abgeschirmte elektrostatische Wechselwirkung sich asymptotisch bis zum Grenzfall harter Kugeln reduziert [6].
Komplexe Plasmen verhalten sich als Einphasen-Flüssigkeit wenn die Wechselwirkung zwischen den Staubpartikeln dominiert, aber auch eine mit Teilchen überladener Zweiphasen-Flüssigkeit ist möglich (wenn die Wechselwirkung mit dem Hintergrundmedium - dem Neutralgas - in ähnlicher oder höherer Größenordnung liegt). In Abbildung 2 ist dies veranschaulicht durch die Konturen der konstanten Verhältnisse von Staub-Staub/Staub-Hintergrund-Impulsübertragungsraten ν_dd/ν_nd im (Γ_ES , κ) Parameter-Raum (Herleitung von ν_dd siehe [6]). Wenn der Impulsübertrag zwischen den Staubpartikeln untereinander über den Impulsübertrag zwischen Staub und Hintergrundmedium dominiert (also ν_dd/ν_nd >> 1), dann verhält sich das System wie eine einphasige Flüssigkeit. Zweiphasige Flüssigkeiten belegen das Regime um ν_dd/ν_nd ~ 1, und mit Partikeln angereicherte Flüssigkeiten erhält man für ν_dd/ν_nd < 1. Im extremen Grenzfall von sehr kleinem ν_dd/ν_nd erhält man lediglich Partikel die die Bewegung des Hintergrundmediums mit nachvollziehen.

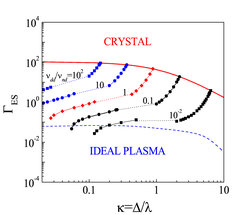
Abbildung 2 zeigt, dass es einen weiten Bereich von Parametern gibt, in dem Komplexe Plasmen die Eigenschaften einer Einphasenflüssigkeit haben. Gleiches gilt auch für Zweiphasenflüssigkeiten. Bedenkt man, dass eine Anzahl von Plasmaparametern (wie z.B. der Neutralgasdruck, die Plasmaabschirmlänge oder das Verhältnis a/λ) sehr leicht um etwa eine Größenordnung variiert werden kann, so wird klar, dass die meisten möglichen Zustände auf kinetischem Niveau untersucht werden können.

3. Komplexes Plasma als nicht-hamiltonisches System

Viele Probleme der Kinetik werden mit dem Hamilton-Formalismus behandelt. Andererseits ist die nicht-Hamilton’sche Kinetik wesentlich weniger gut entwickelt, da solche Systeme weniger Aufmerksamkeit erhalten haben (obwohl sie allgegenwärtig sind) und gewöhnlich durch Trennung der Zeitskalen und dann durch Rückgriff auf den Hamilton-Formalismus bewältigt wurden.
Die Ladung der Staubpartikel in Komplexen Plasmen ist nicht konstant, sondern fluktuiert zeitlich um einen Gleichgewichtswert, der wiederum eine Funktion der räumlichen Koordinaten ist [1,8]. Die Zeitskala der (Ladungs-) Fluktuation und die mittlere Ladung hängen im Allgemeinen vom Ladungsmechanismus des jeweiligen Plasmas ab (vgl. dazu z.B. [9]).

Die eigentliche Besonderheit von Partikeln mit variabler Ladung ist die Tatsache, dass bei Stößen die Energie nicht erhalten bleibt, da die Ladungsvariationen während der Stöße Fluktuationen der Kräfte unter den Partikeln verursachen. Der Grund dafür ist der Folgende: Geladene Teilchen können als Subsystem von Elementarladungen (Elektronen und Ionen) betrachtet werden, die an den Staub gebunden sind, der zusammen mit dem Subsystem der freien Plasmaladungen ein komplettes Ensemble von Ladungen bildet. Selbst wenn das gesamte Ensemble genau ausgewogen ist und als Hamilton’sches System betrachtet werden kann, gibt es einen kontinuierlichen Austausch von Energie zwischen diesen beiden Subsystemen - über den Ladungsprozess - sodass die geladenen Staubpartikel nicht durch eine Hamilton-Funktion beschrieben werden können. Und man sollte natürlich daran denken, dass der Energiefluss in das gesamte (dissipative) System immer durch externe Quellen (wie z.B. inhomogene Ionisation, UV-Strahlung, etc.) gespeist wird - ein Komplexes Plasma ist ein thermodynamisch offenes System. Falls die Fluktuationen der Ladung stark genug sind, ist dafür die Benutzung der thermodynamischen Potenziale zur Beschreibung des Komplexen Plasmas nicht mehr gültig. Der kinetische Ansatz ist ein geeigneter Weg um die Entwicklung der Fluktuationen zu untersuchen. Um die Eigenschaften von Partikelensembles mit variablen Ladungen aufzuzeigen wollen wir den einfachsten Fall annehmen, nämlich dass keine externen Felder vorhanden sind. Dann ist die Kinetik der Partikel ausschließlich durch wechselseitige Stöße bestimmt.
Als ein Beispiel für ein nicht-Hamilton’sches Ensemble untersuchen wir die Kinetik von Partikeln mit einer ortsabhängigen Verteilung der Gleichgewichtsladung. Dies entspricht formal dem Grenzfall unendlich kurzer Ladungszeit [9]. Wenn der Gradient der Ladung grad(q) klein genug ist, also ε=|grad(q)/q|λ << 1, dann ist die relative Änderung der Partikelenergie bei Stößen ebenfalls klein [10]. Dann kann man das Stoßintegral in zwei Teile aufspalten - entsprechend der Änderung des Betrags des Impulses und der Änderung der Richtung des Impulses. Den ersten Teil kann man dann in einer differentiellen Fokker-Planck-Form darstellen, separiert nach dem Kleinheits-parameter ε. Die Analyse der daraus resultierenden kinetischen Gleichung zeigt, dass die mittlere thermische Energie des Ensembles T im Laufe der Zeit anwächst, also die kinetische Temperatur steigt. Als hinreichende Bedingung für eine Aufheizung erhält man ν_nd ≤ ε²ν_dd. Bei Auftreten einer Instabilität divergiert die Temperatur zu einem endlichen Zeitpunkt, da T~ (1-t/t_cr)^-2, mit t_cr~1/(ε²ν_dd). Deshalb erhält man für Ensembles mit variablen Ladungen ein explosionsartiges Anwachsen der Energie.
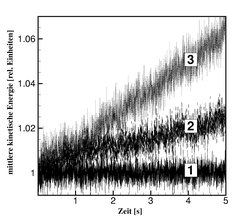
Um diese theoretischen Ergebnisse zu verifizieren haben wir eine 2D-Molekular-Dynamik-Simulation eines Yukawa-Systems von Partikeln mit variablen Ladungen durchgeführt. Dazu haben wir 5000 Partikel zufällig über eine Quadrat der Seitenlänge L=1cm mit einer anfänglich isotropen Maxwell’schen Geschwindigkeitsverteilung verteilt, wobei die Ladungen linear von der z-Koordinate abhängen. Dabei ist q=3·10³e an der linken Grenze z=0. Wir haben periodische Randbedingungen für die Partikelgeschwindigkeiten gewählt (an den Rändern z=0 und z=L). Die hierzu orthogonalen Rändern y=0 und y=L sind reflektierend. Die Abschirmlänge der Yukawa-Wechselwirkung ist λ=30µm (etwa ein Drittel des mittleren Teilchenabstands). Abbildung 3 zeigt die mittlere kinetische Energie der Partikel (auf die Anfangstemperatur normiert) als Funktion der Zeit für verschiedene Werte des Ladungsgradienten ε. Wie erwartet bleibt die mittlere Energie ohne Gradienten konstant. Für endliche ε skaliert die Energie zunächst mit ε²t. Die numerisch berechnete Größe des Energieanstiegs deckt sich ebenfalls mit den theoretischen Vorhersagen.

4. Schlussfolgerungen

Es gibt eine ganze Anzahl von Gründen, warum Komplexe Plasmen von großer Bedeutung für die Grundlagenforschung sind. Die Ergebnisse aus Kapitel 2 zeigen, dass Komplexe Plasmen für die Erforschung kritischer Phänomene besonders geeignet sind. Zum Beispiel kann man die Kinetik von Kristallisation und Schmelzen in Echtzeit untersuchen. Die Keimbildung und das sich anschließende Wachstum kristalliner Strukturen in Komplexen Plasmen sieht dem gewöhnlichen Kristallwachstum (z.B. bei Halbleitern, vgl. [11,12]) sehr ähnlich. Deshalb können Raum-Zeit aufgelöste Messungen der Elementarprozesse, die die Keimbildung und das Wachstum von Plasmakristallen begleiten, hilfreich sein für das Verständnis einiger grundlegender mikroskopischer Prozesse bei flüssig-festen Phasenübergängen. Ferner bieten Plasmakristalle eine gute Möglichkeit, transport-relevante Wellenphänomene in gewöhnlichen Kristallen (Z.B. Wärmeleitung), ebenso wie nichtlineare Modenwechselwirkungen, Umklapp-Prozesse, sowie Phononenstreuung an Fehlstellen etc. auf kinetischer Ebene zu erforschen.
Komplexe Plasmen im Labor sind hervorragend dafür geeignet, kinetische Studien von Elementarprozessen in Flüssigkeiten zu betreiben [13]. Vergleiche hinsichtlich dimensionsloser Ähnlichkeits-Parameter - Reynolds- und Machzahlen - legen nahe, dass Komplexe Plasmen konventionellen Flüssigkeiten (wie Wasser) in vieler Hinsicht auffallend ähnlich sind - allerdings, und das ist einzigartig, auf "molekularer Ebene" beobachtet. Dies impliziert, dass wir offenbar ein mächtiges neues Werkzeug für die Erforschung von Flüssigkeitsströmen auf (in gewissermaßen) Nanoskala haben, das den ganz wichtigen Übergang vom kollektiven Flüssigkeitsverhalten zum sich kinetisch verhaltenden Einzelteilchen ebenso einschließt, wie nichtlineare Vorgänge auf Skalen, die bislang experimentell noch nicht zugänglich waren.
Ohne Zweifel, die Physik - insbesondere die kinetische Physik - hat schon großen Nutzen von der detaillierten Erforschung der Kinetik Komplexer Plasmen gezogen, eine Entwicklung die in der Zukunft noch wichtiger sein wird. Seit der Entdeckung der "Plasmakristall" in 1994, wird das in ca. 3000 Veröffentlichungen weltweit dokumentiert, wobei das Arbeitsgebiet sich ca. alle 3 Jahre verdoppelt hat.

Literaturverzeichnis

[1] V. N. Tsytovich, Physi k Uspekhi 40, 53 (1997).
[2] G. E. Morfill et al., Physica Scripta T107, 59 (2004).
[3] G. E. Morfill et al., Plasma Physics Controlled Fusion 44, B263 (2002).
[4] J. Chu und L. I, Physics Rev. Letters 72, 4009 (1994).
[5] H. Thomas et al., Phys. Physics Rev. Letters 73, 652 (1994).
[6] S. A. Khrapak, A. V. Ivlev und G. E. Morfill, "Momentum transfer in complex plasmas", eingerichtet an Physical Review E (2004). to be published.
[7] O. Vaulina, S. A. Khrapak und G. E. Morfill, Physical Review E 66, 016404 (2002).
[8] V. V. Zhakhovskii et al., JETP Letters 66,419 (1997).
[9] S. A. Khrapak et al., Physical Review E59, 6017 (1999).
[10] A. V. Ivlev et al., "Kinetics of ensembles with variable charges", eingereicht bei Physical Review E (2004), to be published.
[11] B. Voigtländer et al., Physics Rev. Letters 78, 2164 (1997).
[12] M. Kästner et al., Physics Rev. Letters 82, 2745 (1999).
[13] G. E. Morfill et al., Physics Rev. Letters 92, 175004 (2004).